どうも皆さま、約一週間ぶりの掲載となりますが先週の「天皇賞・春(G1)」はいかがだったでしょうか。
残念ながら先週は家業があまりにも多忙だった影響で解説記事を準備する時間がありませんでした。(分析は終えていましたが、文章とグラフを用意をする暇がなかったのです)
今週の「NHKマイルC(G1)」はおそらく準備できると思いますので、どうかお楽しみにしてください。
さて、今回のコラムは、だいぶ前に掲載した「3歳限定戦の解説をなぜしないのか https://keibaanalysis.com/archives/358 」という件に関しての記事の検証記事になります。
ここ最近では「3歳限定戦」の解説記事も掲載していますが、タイム指標の基となるデータベースを構築できたため解説を行うようになったからです。
それまでの方針は「馬齢限定戦」と「馬齢オープン戦」ではそもそも「実力」の「ばらつき具合」に違いがある、つまり「馬齢オープン戦」よりも「馬齢限定戦」の方が実力差が大きく出やすいので「レース傾向」との相性が比較的に重視される「馬齢オープン戦」の解説のみを行うという形でした。
今回はその「ばらつき具合」を数値的に検証した記事になります。内容としては短いものになりますが、データの収集とその結果の意義は非常に重要なものになりました。
「ばらつき具合」をどう比較するのか?
まず始めに、「実力」の「ばらつき具合」をどう比較すればいいのかという話です。「実力」を数値として示せるものとしては、単純に考えれば「走破タイム」・「上がりタイム」の二つのデータが挙げられ、データとしての扱いやすさ・収集のしやすさを加味すればそれら二つのデータを「実力」の数値的なデータとするのが妥当と言えます。
「ばらつき具合」は調べる方法としては、統計学には「分散」や「標準偏差」などの指標がデータの「ばらつき具合」を推し量る数値がいくつかありますが、「走破タイム」・「上がりタイム」は「距離」はもちろん「競馬場」・「馬場状況」によって変動するという問題があります。
「分散」や「標準偏差」は数値の大小に応じて変動する指標なので、それらを使って単純に比較をすることはできないのです。
そのため、比較するための指標として用いるのが「変動係数」です。
「変動係数」は「標準偏差/平均」で計算される数値で、「標準偏差」が「平均」のどの位を占めているのかを表しています。
これを用いれば「距離」・「競馬場」・「馬場状況」が違っていたとしてもばらつきの具合を比較し合うことが可能になります。
というわけで、過去5年間:2019~2023年(京都競馬場は2017~2020年及び2023年) にJRAで行われた各芝レースの「走破タイム」・「上がりタイム」の「変動係数」を計算し、
・「2歳限定戦」
・「3歳限定戦」
・「3歳以上戦」
・「4歳以上戦」
の年齢制限ごとに「平均変動係数」を測定しました。
「平均変動係数」を比較すると…
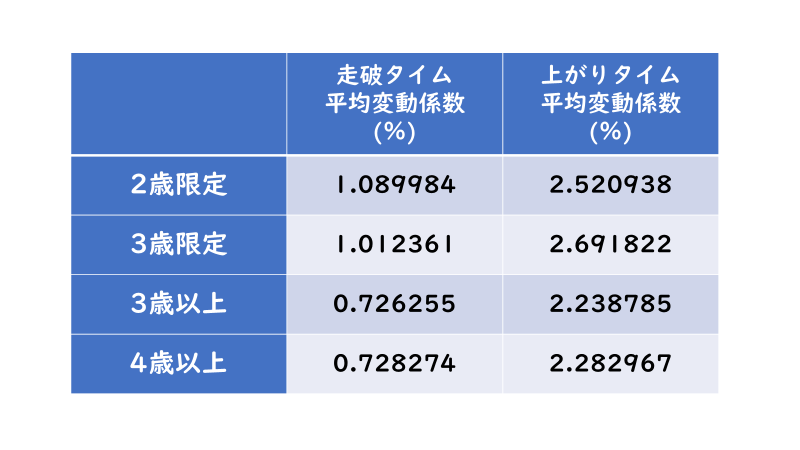
上の表が各年齢制限ごとの「平均変動係数」になります。見事に「馬齢限定戦」の方が「馬齢オープン戦」に比べて「平均変動係数」が高い=タイムのばらつきが大きいという結果になりました。数値で見ると「走破タイム」は約「0.3」%、「上がりタイム」は約「0.4」%ほど差があります。
1%未満の差なので誤差と思ってしまう方がいるかもしれませんが、各年齢制限の「東京・芝2000・良」の条件での「平均走破タイム」を参照して上表の「平均変動係数」を当てはめた想定を行うと、「馬齢限定戦」は1位と最下位の走破タイムの差が約「4.0」秒、「馬齢オープン戦」は1位と最下位の走破タイムの差が約「2.8」秒となり、明確に「馬齢オープン戦」の方が約「1.2」秒もタイム差が狭いということが分かります。
このように「タイムの変動係数」は「走破タイム指標」・「上がりタイム指標」のようにレースごとに変動する要素であり、それら指標をより正確に評価する上で必要な要素でもあります。
今回データの収集を行うこともできたため、今後の「タイム指標」の分析にはこの「タイムの変動係数」による補正を加えた上で調べていきたいと思います。
今回の記事は以上になります。ご閲覧ありがとうございました!



