どうも皆さま、今回は「人気順ごとの基準オッズ」に関しての解説を行っていきます。
以前の「オッズ」解説の記事で「人気順」が下に行くほど「オッズ」が指数関数的に上昇していくという話をしましたが、具体的に順位が一つ下がるとどのくらい「オッズ」は上昇するのかには触れませんでした。
本記事ではレースデータを活用しながら「人気順」と「オッズ」の関係性を説明したうえで、「人気順に対してオッズがどの程度であれば適正なのか」を解説していきます。
「人気順」と「オッズ」の関係性とは?
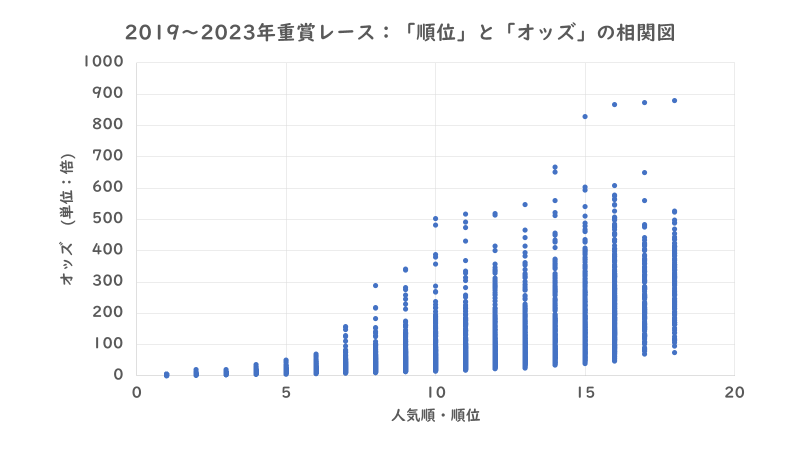
まずは上の「相関図」を見てください。これは2019年~2023年の5年間にJRAが開催した重賞レースに出走した馬の「人気順」と「オッズ」を「相関図」にしたものです。
見ての通り「人気順」が下位に行くほど「オッズ」は上昇していき、順位ごとの「オッズ」の幅も下位に行くほど広がっていくことも分かると思います。
より傾向が分かりやすくなるように、各順位の「最小値」・「中央値」・「最大値」のオッズを抜き出した「相関図」を作ると以下のようになります。
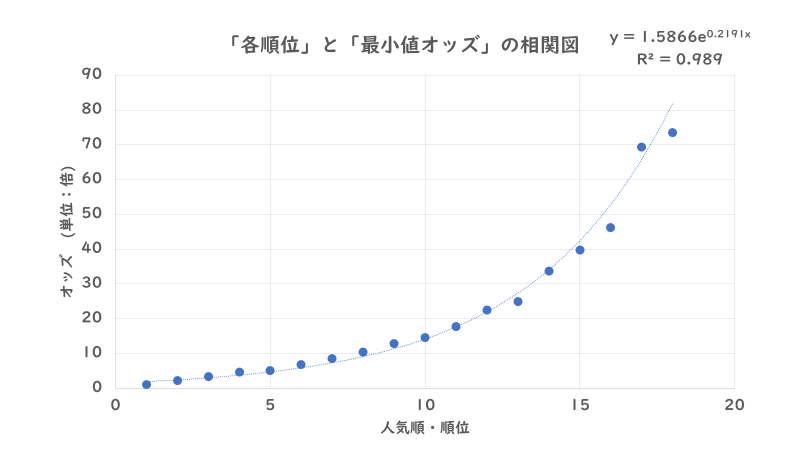
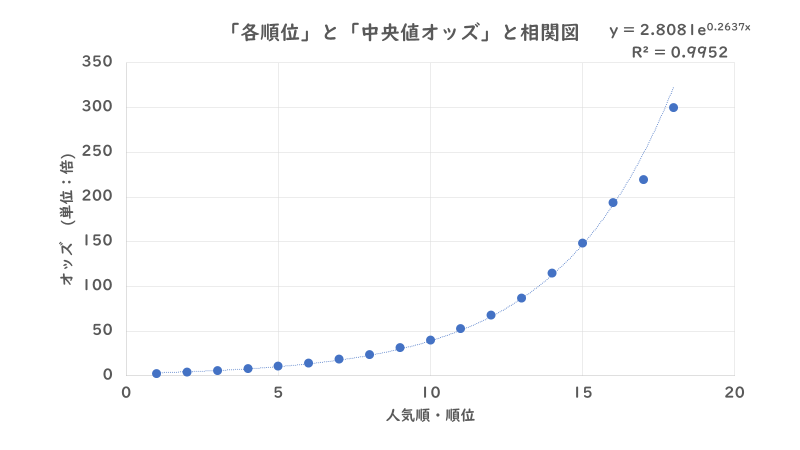
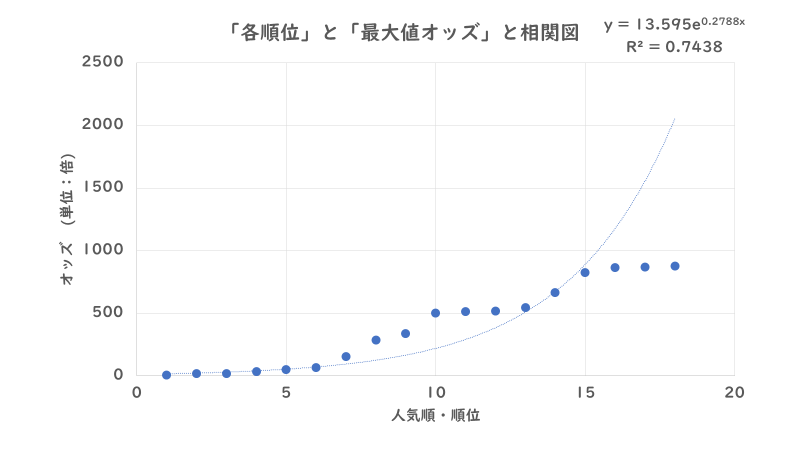
いかがでしょうか。「最小値」・「中央値」の相関図に関しては非常にはっきりとしていますが、指数関数的に「オッズ」が上昇していることが分かります。
また、グラフの上に記載されている指数近似曲線の式は「オッズ=A×e(=ネイピア数)^(B×人気順の順位)」で表記されていますが、変換すると「オッズ=A×(e^B)^人気順の順位」となります。
ここで各グラフの「e^B」を計算すると以下のようになります。
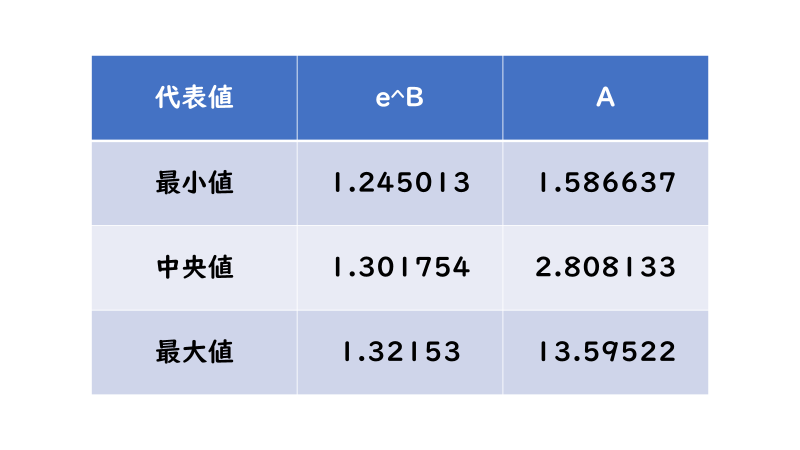
「e^B」の値がAの値に比べると幅が小さく「1.3」に近い値になっていることが分かります。より詳細にいくつかの代表値を取り上げて調べた結果、基本的にこの「e^B」の値は約「1.3」になることが判明しました。つまり、大抵の「オッズ」が式「オッズ=A×1.3^(人気順の順位)」に則っているということになります。
補正を加えて近似式を調べると?
ここで補正を加えた上で新たに相関図を作り、指数近似曲線の式を調べました。上述の計算式では「オッズ」の値が理論上の最小値「0.8」を下回る場合があるので、補正をする必要があるのです。
補正というのは、「オッズ」の「理論上最小値」と「人気順」の「最高順位」の二つです。単勝馬券の「オッズ」は理論上の最小値は「0.8」倍であり、人気順の最高順位は「1」位なのでこれらの値を考慮します。補正を加えた近似式は「オッズ–0.8=A×(e^B)^(人気順の順位–1)」になります。
基本的な相関図の分布は上述のグラフと同様になるので割愛しますが、近似式の「e^B」と「A」の値は以下のようになります。
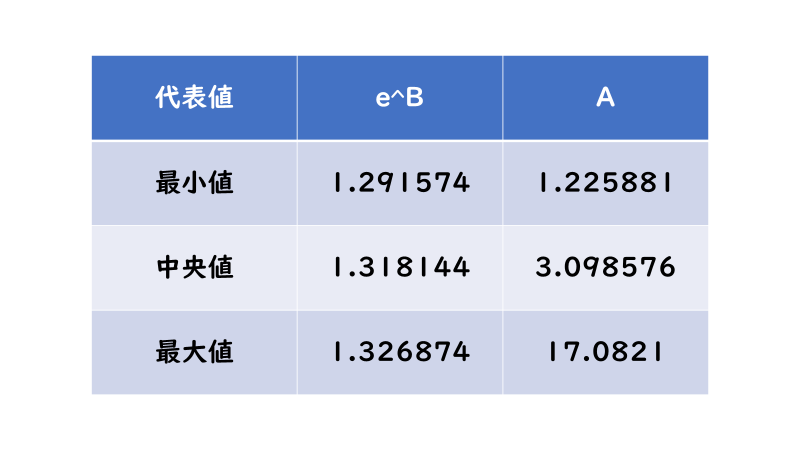
基本的には上述の表と同じく「e^B」の値が約「1.3」になり、他の代表値の近似式も調べた結果「e^B」はほぼ「1.3」になることが分かりました。
よって補正式も「オッズ–0.8=A×1.3^(人気順の順位–1)」になります。
「A」の値はどのように分布しているのか?
ここで、上述の式に入る「A」の値に注目しましょう。ここの値に関しては各順位の代表値の相関図を用いても規則性を見出すことが出来なかったため、式を「A=(オッズ–0.8)/1.3^(人気順の順位–1)」と変換することで、各馬の「人気順の順位」と「オッズ」から「A」の値を計算し、代表値の測定と度数分布化を行いました。
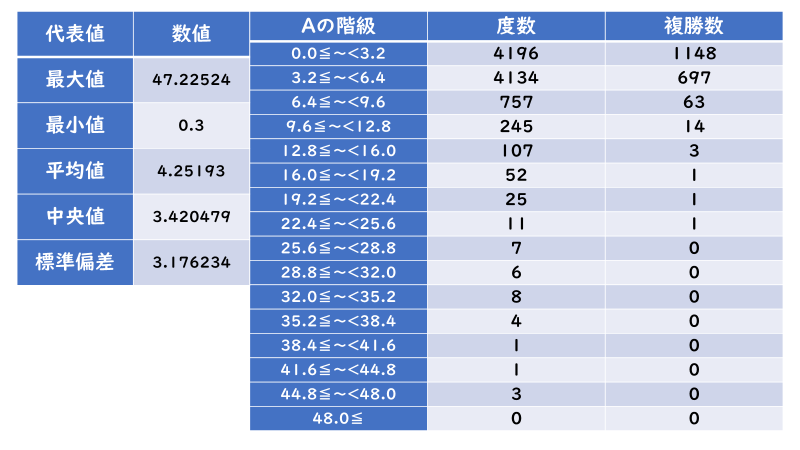
いかがでしょうか。大半の「A」の値が「0.0≦~<6.4」に分布しており、「複勝数」の分布は「A」の値が大きくなるほど低下していく傾向であることが分かります。そのため、基本的には「A」の値が「6.4」の時の「オッズ」を「基準オッズ」とし、それよりも大きいか小さいかで「オッズ」が適正であるか判断することが適切であると言えます。
「基準オッズ」を見てみよう!
上述の「A」の値「6.4」を式に代入すると「オッズ–0.8=A×1.3^(人気順の順位–1)」となり、変換すると「オッズ=A×1.3^(人気順の順位–1)+0.8」になります。
ここから、各順位の「基準オッズ」を計算すると以下のようになります。(オッズの値は四捨五入した値になってます。)
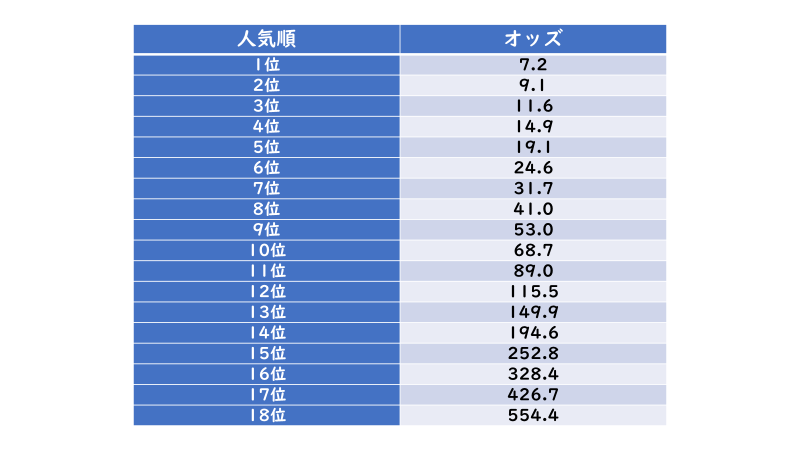
基本的に「人気順」が「1位」の場合はほぼ確実に適正になると考えられますが、「2位」以降に関しては人気の集中具合によってはこれらの「基準オッズ」を上回る可能性が十分に考えられ、人気順上位だったとしても危ない可能性があります。
逆に言えば、例え人気順下位の馬だったとしてもこれらの「基準オッズ」を大きく下回る場合はむしろ大穴となる可能性が高いとも言えます。
もちろんこれらはあくまでも目安なので「基準オッズ」と多少の差であればそれほど気にしなくていいと思いますが、値が大きく乖離している場合はよくチェックしておくべきです。
まとめ:「基準オッズ」との差をチェックしよう!
いかがだったでしょうか。今回は「人気順ごとの基準オッズ」に関しての解説を行いました。過度に気にするようなデータではないのですが「オッズ」を適正を測るという意味では非常に需要な要素です。穴馬を探す上では比較的に重宝できるデータであると思うので、是非とも活用してみてください。
今回の記事は以上になります。閲覧ありがとうございました!!



