今回の記事は、「人気順」と「オッズ」に関しての競馬統計解説になります。
どちらもレースに密接に関わってくるデータではありますが、実は統計分析をする場合には取り扱い注意なデータになってきます。(今回は「単勝人気順」と「単勝オッズ」を前提に話を進めます)
「人気順」と「オッズ」とは?
「人気順」と「オッズ」は直接的な関係のあるデータです。
単勝馬券で説明する場合、「オッズ」は「0.8/単勝支持率 (単位:倍)」で計算される数値で、単勝馬券を1点で買った時に何倍で払い戻されるか?を表しています。
「単勝支持率」というのは「各馬の単勝馬券の売上/全体の単勝馬券の売上」で計算される数値で単勝馬券全体の何割がその馬を買っているのか?を表します。
本来は「オッズ」=「支持率の逆数(=1/単勝支持率)」という形になるのですが、中央競馬の場合は単勝馬券の総売上の80%が払い戻しの対象になるので分子は1では0.8で計算する必要があります。
「人気順」は「オッズ」を昇順にして順位付けしたデータです。つまり、オッズが小さいほど順位が高くなり大きいほど順位が低くなります。
基本的に多くの競馬情報サイトでは「人気順」の統計を取って傾向を調べていることが多く、「オッズ」が適切に統計分析されることは比較的に少ないです。
しかし、「人気順」の統計を取って傾向を調べるのは分析として不適切です。
「人気順」は「非数値データ」・オッズは「数値データ」
「人気順」と「オッズ」はどちらも数字で表されるデータなのですが、データの種類としては全く違います。
上述した通り、「オッズ」は計算式で表すことができるので「数値データ」になります。
一方で、「人気順」は「オッズ」を元に順位付けしたデータです。「順位付け」というのは順序に従って「番号」を割り振るということです。
「番号」というのは「数値」ではありません。他のデータとの大小関係や位置関係を識別するためのマークのようなものです。その為、「人気順」は数値データではなく「非数値データ」になります。
(以下は数学のテスト結果の例)
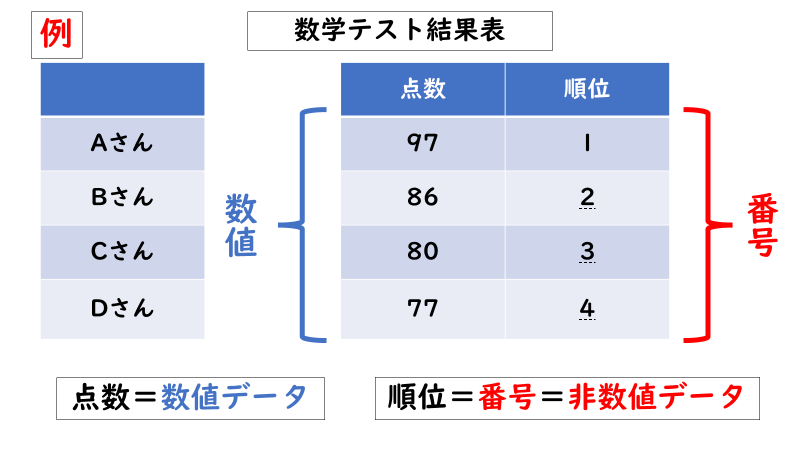
「人気順」以外にも「非数値データ」は競馬データにいくつもあります。「枠番」や「性別」なども計算式で表すことはできないので、それらも「非数値データ」に区分されます。
しかし「人気順」がそれら違う点として、元となるデータの「オッズ」=「数値データ」の存在があります。各オッズの大小関係を分かりやすく番号付けしたのが「人気順」であって、番号そのものに意味があるわけではないのです。
そのため、「人気順」の統計を取ることは適切ではないのです。あるレースで順位が低い数値だとしても他レースではその順位より上になっているというように相対的に変動する要素なので統計を取る意味が薄いのです。
「オッズ」の正確な統計方法とは?
それでは、「オッズ」の統計とはどのように取ればいいのでしょうか?
基本的には「数値データ」であることを活かして「度数分布表」を用いるのが一番でしょう。
「度数分布表」というのはデータ全体を一定間隔ごとに区間を分けていき、各区間ごとにいくつデータがあるか調べていき表にまとめる方法です。
例えば「馬体重」を「度数分布表」にまとめると以下のようになります。
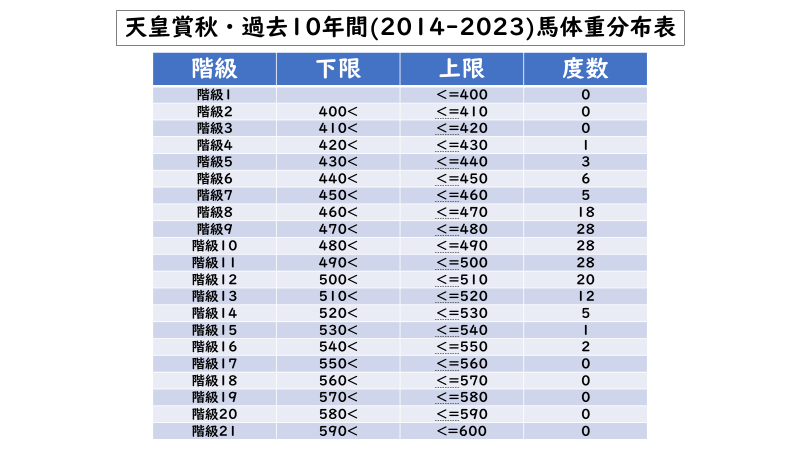
「度数」というのは「データの個数」のことです。この表の場合、「470~480Kg」・「480~490Kg」・「490~500Kg」の3階級で「データの個数」が最多になりました。
そして、それらを頂点として上の階級も下の階級も「データの個数」が減少していくことがわかりますね。グラフにしてより視覚的に見てみましょう。
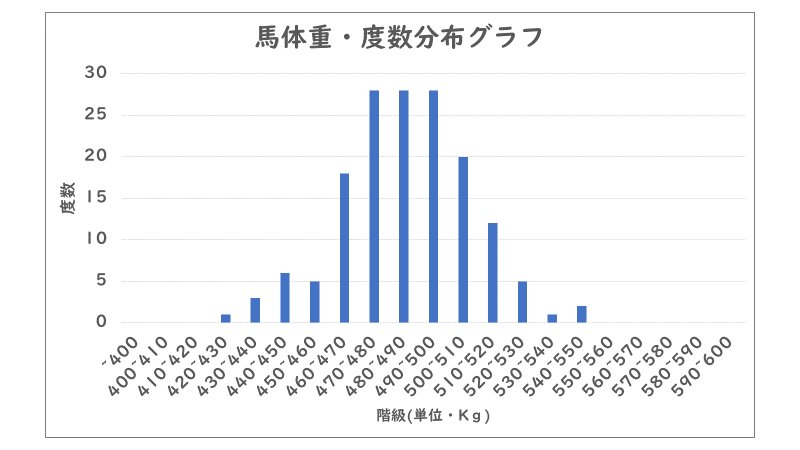
比較的きれいな山形になったと思います。他のレースでの馬体重のデータを統計で調べてみても、このような山形になりやすいです。よりはっきりときれいな山形になると「ガウス分布」とよばれるグラフになり、基本的に馬体重の度数分布表は「ガウス分布」に近いグラフになることが多いです。
「ガウス分布」に近いグラフであれば「ガウス分布」の法則性などを応用することができるおかげで分析がしやすく、統計分析としては非常にありがたいものです。
しかし、すべての度数分布がこのような分布になるわけではなく、「オッズ」の度数分布に関しても「ガウス分布」に近いグラフにはならないのが難しいところなのです。
オッズの分布の仕方
実際に上述の馬体重と同じ方法で「オッズ」の分布を調べてみると以下のような表になります。
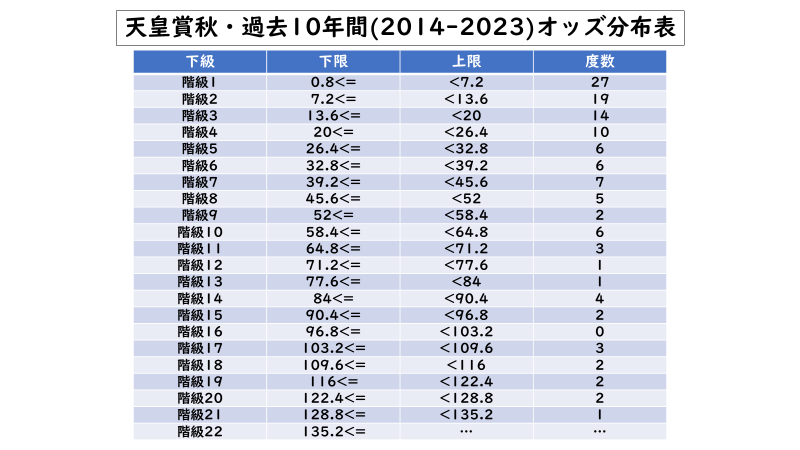
これが階級の幅を「6.4」に設定した場合の度数分布表になりますが、これは表の一部になります。天皇賞秋における過去10年間でのオッズの最大値は「406.1」なのでこの階級の幅では階級の数は60以上になるのです。上の馬体重の度数分布表ように階級の数が20個ほどで済むようにするには階級の幅をおよそ「20」に設定しなければなりません。
しかし、階級の幅が「20」になるということは「人気順」で例えるならば1番人気と7番人気くらいを同じ階級で数えているということになりかねません。(16頭立てのレースだったならば半数近くが同じ階級になるということです)
さらに上の馬体重の度数分布表と比較すると、一番上の階級の度数が最大で徐々に減っていく傾向になっており、「ガウス分布」に近いグラフになるとは考えられません。
なので「馬体重」と同じやり方の「度数分布表」ではオッズの分析は難しくなるのです。
そのために、「オッズ」の「度数分布表」を作る時は「階級の幅」の設定に工夫を行うのです。
オッズのための度数分布表:「等比」的な階級の幅
馬体重の度数分布表の場合は「階級の幅」を同じ幅の長さに設定しました。つまり、「等差」的な間隔であったということです。「オッズ」の場合は最小値と最大値の差が大きくなってしますのでこの「等差」的な間隔では上手くいかないのですが、一定間隔の幅の取り方にはもう一つ「等比」的な間隔というのもあります。
「等比」というのは一定間隔ごとに比例していくということです。つまり、「等比」的な階級の幅というのは一番最初の階級の幅から下の階級であればあるほど比例した間隔を取っていくということです。
具体的な例としては以下のようになります。
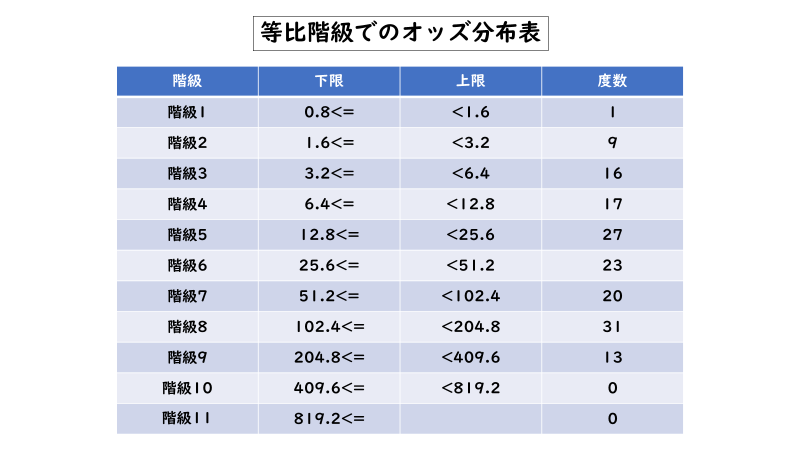
この方法であれば一定間隔の幅を維持でき、かつ階級の数が多くなることを避けることができます。また、「馬体重」の度数分布表とまではいきませんが、等差階級的な度数分布よりも「ガウス分布」に近くなります。
まとめ:オッズは等比階級な度数分布で調べよう
というわけで、今回は「人気順」と「オッズ」についての記事でした。
あくまで「人気順」は「オッズ」の昇順を分かりやすくしたもので、数値的な扱いをするべきではありません。統計的に調べるならば「オッズ」を重視した方がいいです。
「オッズ」に関しても普通の度数分布表では分析しにくいため、階級が下へ行くほど「階級の幅」が比例していく「等比階級による度数分布表」を使うと分析しやすくなります。
データの種類や分布によっては扱い方に工夫が必要ということですね。
今回は以上になります。閲覧ありがとうございました!!



