今週末に行われる「中山記念」の過去データを集計しながら、ふと思いました。
過去の記事で「馬体重」・「馬体重増減率」・「斤量馬体重比率」など、数値データに関しては「度数分布表」を用いて分析を行ってきました。実際にこれらの数値データは全体的には正規分布に近いグラフになる傾向があるため非常に有効ではあります。ところが、実を言うと「度数分布表」の階級は今まで「なんとなくの幅で決めてしまっていた」のです。
というわけで、今回の記事は反省メモ「階級の幅の修正」と題して、統計的なデータで用いて「階級の幅の決定方法」を解説していき、各数値データの「度数分布表」の「階級の幅」を修正していきます。
まず度数分布表とはどんなものだったか?
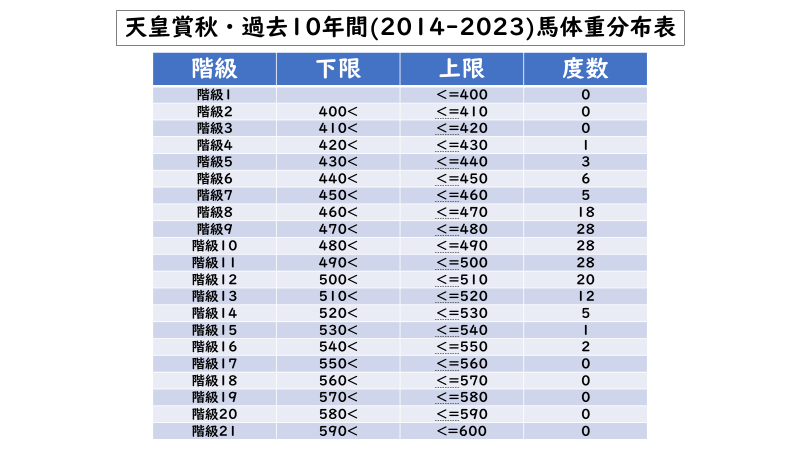
改めてになりますが、「度数分布表」とはどんなものだったか説明していきます。
「度数分布表」とは基本的には調べるデータ全体を一定幅の「階級」に分け、各階級の「データの個数(度数)」を数えて表化したものです。上の例は天皇賞秋過去10年間の馬体重の「度数分布表」で、各階級の幅を「10」kgとして分布を調べています。
「オッズ」についての記事を書いた際に「馬体重」の分布に関して触れましたが、「馬体重」は基本的に「正規分布」(平均値・最頻値・中央値が一致した山形のグラフ)に近い分布になり、上の表に関してもグラフ化すると
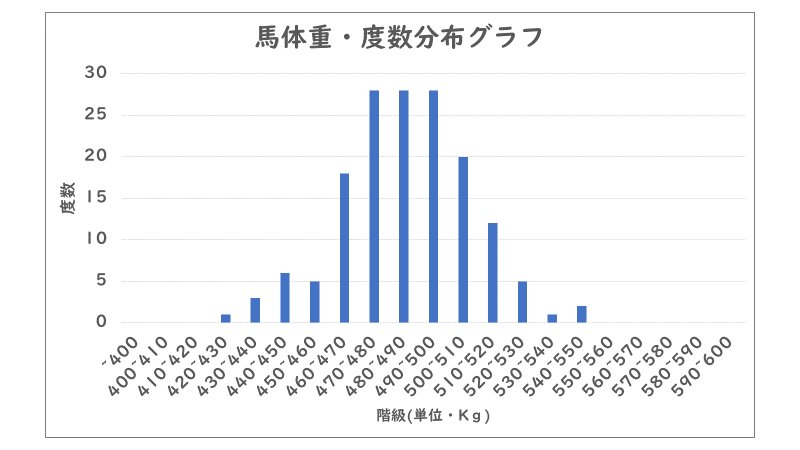
このように比較的にきれいな山形を形成します。現在の「10」kgの幅の時点で「全体の分布傾向」を分析することは可能であり、「階級の幅」があまりにも広すぎない限りはどの程度であってもさほど大きな差は生じません。
問題は「複勝率の傾向」を分析するときです。「階級の幅」が狭いと各階級の「データの個数」が少なくなってしまうため、「階級」ごとのデータの信用性が低下してしまいます。
実際に「階級の幅」が「5」kgと「10」kgの場合の「馬体重」の分布と「複勝率」のグラフは以下のようになります。
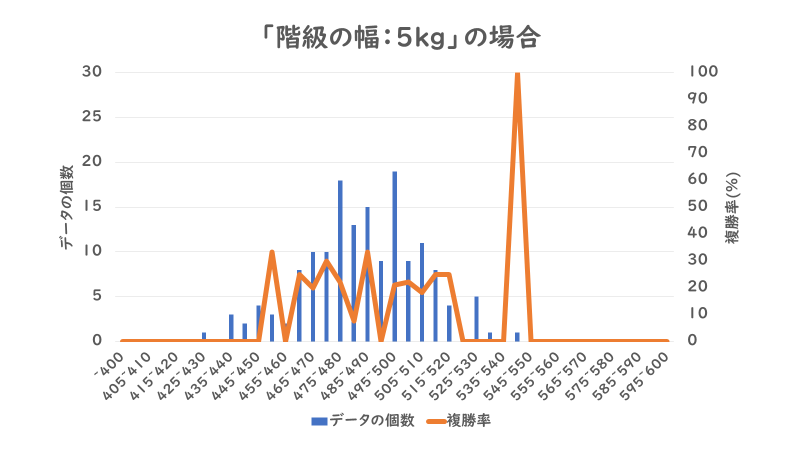
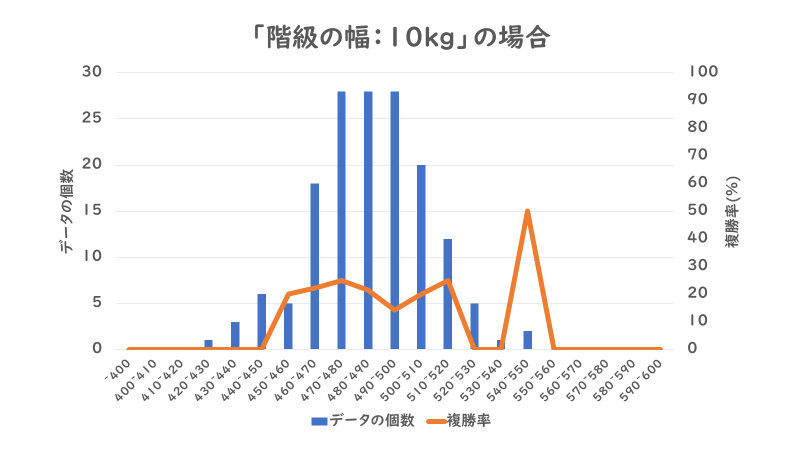
グラフを比較してみると、「5」kgの場合の方が各階級の「データの個数」が少なくなり、「複勝率」のグラフの形はギザギザとして振れ幅が大きいことが分かります。「複勝率」が上昇し始める境目を詳細に特定しやすくなりますが、階級ごとの振れ幅が大きくなり「複勝率」の信用度が下がるのです。
このように「複勝率」の傾向を調べる場合は「階級の幅」をどの程度にするかが重要になってきます。そして、この「階級の幅」は統計的な方法である程度見積もることができ、そのために用いるのが「標準偏差」になります。
「階級の幅」の決定方法:標準偏差
標準偏差とは?
「標準偏差」は中学・高校時代に数学の授業で聞いた言葉であると思います。どういうものか何となくでしか覚えてないかもしれませんが、一言で言えば「分散の平方根」となります。
「分散」とは統計データの一つで「データ全体がどのくらい散らばっているか?」を表しています。「分散」の値が大きいほど「データの散らばりが広い=データの振れ幅が大きくなっている」、「分散」の値が小さいほど「データの散らばりが狭い=データの振れ幅が小さくなっている」という形になっています。
そのため、「分散」はデータの分布傾向を調べる上で非常に重要な要素になっていますが、一方で欠点も存在しています。
それは、「具体的にどれくらいの振れ幅なのかが分からない」という点です。これは「分散」が各数値データを「二乗」して計算していることが原因で、つまり「分散の平方根」を求めれば具体的にどれくらいの振れ幅であるのかが分かるのです。
それが「標準偏差」になります。「標準偏差」は「各データが平均値から大体どの程度離れているか」を表している統計データで、例えば「標準偏差」が「10」であった場合、大体のデータは平均値から「±10」の間に収まっていることが分かるのです。
ではなぜ「標準偏差」が「階級の幅」に用いるのかというと、これは「馬体重」に関わるデータ全体が「正規分布」に近くなるという点が重要になってきます。
というのも「正規分布」は「標準偏差」を幅とした区間を用いてデータの信頼度を推定しているのです。そのため、「標準偏差」を基準に「度数分布表」の「階級の幅」を決定することは理に適ったことなのです。
各種データの標準偏差はどうなってるのか?
というわけで、実際に各種データの標準偏差を見ていきましょう。
「馬体重」・「馬体重増減率」・「斤量馬体重比率」の3項目に関してG1・4レースの過去5年間のデータに基づいて各データの標準偏差を算出しました。(※小数第2位以下四捨五入)
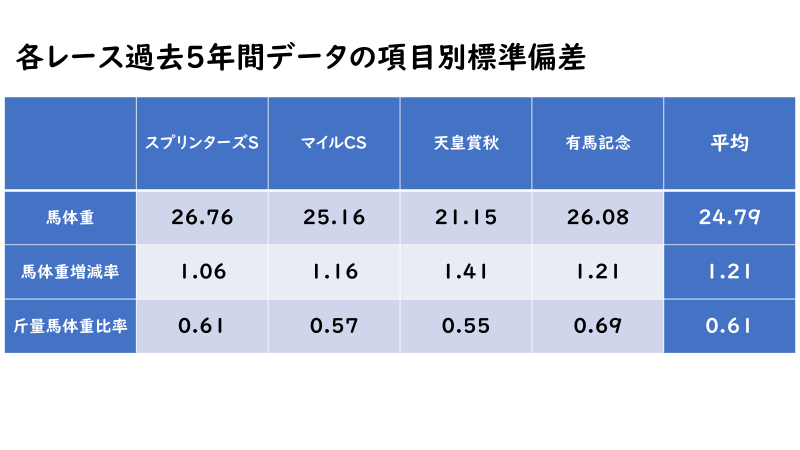
4レースの標準偏差の平均値で考えてみると「馬体重」は「25」前後、「馬体重増減率」は「1.2」前後、「斤量馬体重比率」は「0.6」前後が「階級の幅」として適しているように見えます。実際には数字をちょうどいい区切りにするために「20」・「1.0」・「0.5」とした方がグラフとしては見えやすくなると思います。
もちろんレースごとに「標準偏差」が変わってくるのでレースごと「階級の幅」を変更した方が正確ではありますが、基本的には以上の数値を参考にして問題ないかと思います。
まとめ:「標準偏差」で正確な階級付け
如何だったでしょうか。今回は「標準偏差」を基準にした「階級の幅」の決定についての記事でした。「馬体重」に関わるデータ全体が「正規分布」に近くなるという傾向からこのような形で「階級の幅」を決定しましたが、「オッズ」のような通常では「正規分布」にならないような「度数分布表」では今回の方法は参考にできません。
グラフの特徴や傾向からこのような形で最も適した「階級の幅」を決定することが大事になってきます。それぞれのデータごとによく分析した上で検討をしていきましょう。
今回の記事は以上になります。閲覧ありがとうございました!



