どうも皆さま、今回は「複勝率」にまつわる解説記事になります。
「複勝率」は本ブログの「レース分析記事」においてたびたび傾向の解説のために用いてきた数値データです。なぜ利用してきたのかと言うと数値としてどのようなものなのかイメージしやすく単純な四則演算で計算することができるからです。「解説のため」のデータとしてはうってつけでした。
しかし、実を言うと以前から「複勝率」が直接的に競馬予想に活用できるかは疑念に感じていました。過去に数値のみを用いて順位予測をした際に、「「出走数」に対しての割合(単勝率・連対率・複勝率など)」を表している数値を使った予測では結果と大きく違っていることが多々あったからです。
今回はその疑念を確かめるために「カイ二乗検定」を用いた分析を行い、その結果として「「複勝率」はほとんどの場合において無意味」であることを結論づけられました。
というわけで、本記事ではその「カイ二乗検定」を用いた分析と結果について解説をしていきます。
そもそも「複勝率」には欠陥がある
先にも述べた通り、「複勝率」というのは非常に分かりやすいデータです。
例えばある重賞レースの過去5年間の「枠番」のデータを調べた時、
・「1枠」で出走した馬(出走数)「9頭」の内「複勝」に入った馬(複勝数)「3頭」
・「6枠」で出走した馬(出走数)「10頭」の内「複勝」に入った馬(複勝数)「1頭」
このような状況であったならばそれぞれの「複勝率」を計算すれば
・「1枠」:「複勝率」=「複勝数:3頭」÷「出走数:9頭」×100=「約33.3%」
・「6枠」:「複勝率」=「複勝数:1頭」÷「出走数:10頭」×100=「10.0%」
以上のようになり、比較すれば「1枠」>「6枠」なので「1枠」の方が有利な可能性が高いと言えそうです。計算も「複勝数÷出走数」を百分率で表すだけなので小学生でも簡単に出来てしまい非常に単純です。
一方で、問題も存在しています。上記の例では「出走数」がそれぞれ「9頭」・「10頭」であるためそれほど大きな差はありません。もし、以下の過去5年間の「性別」のデータの場合はどうでしょうか?
・「牝馬」で出走した馬(出走数)「9頭」の内「複勝」に入った馬(複勝数)「3頭」
・「牡馬・セン馬」で出走した馬(出走数)「80頭」の内「複勝」に入った馬(複勝数)「12頭」
先ほどの「枠番」と違い「出走数」に大きな差があります。同じように「複勝率」を計算した場合にどうなるかというと、
・「牝馬」:「複勝率」=「複勝数:3頭」÷「出走数:9頭」×100=「約33.3%」
・「牡馬・セン馬」:「複勝率」=「複勝数:12頭」÷「出走数:80頭」×100=「15.0%」
このように「牝馬」>「牡馬・セン馬」の方が「複勝率」は高いという結果になります。しかし、「出走数」に大きな差があり「複勝数」を比較してみれば「牡馬・セン馬」>「牝馬」となってしまいます。
「複勝率の欠陥」というのはまさにこの点、「母数の大きさの違い」によって単純比較が行えないという問題です。差がそれほどなければ問題となることは少ないのですが、「性別」のデータのように、データの種類によっては大差になってしまうことがしばしばあります。
「出走数」から「複勝数の期待値」を考える
この問題点をどう解決すればいいのか?「「出走数」が大きく違う場合にもし「出走数」が同じであったならば「複勝数」はどうなるか?」、これを推定できればいいのですが非常に難しい話です。
一方で、違う観点で考えると「各属性・項目・階級の出走数」と「合計出走数」が分かればそこから「各属性・項目・階級の予測される複勝数」、つまりは「複勝数の期待値」を計算することが出来ます。
例えば、上述した過去5年間の「性別」のデータの場合、
・「牝馬」で出走した馬(出走数)「9頭」の内「複勝」に入った馬(複勝数)「3頭」
・「牡馬・セン馬」で出走した馬(出走数)「80頭」の内「複勝」に入った馬(複勝数)「12頭」
であるので、
・「過去5年間の合計出走数」=「牝馬の出走数:9頭」+「牡馬・セン馬の出走数:80頭」
=「合計出走数:89頭」
・「過去5年間の合計複勝数」=「牝馬の複勝数:3頭」+「牡馬・セン馬の複勝数」
=「合計複勝数:15頭」
ここで、合計出走数」に対しての「牝馬」・「牡馬・セン馬」の割合と「合計複勝数」の割合を計算します。
・「牝」:「合計出走数に対しての割合」=「9頭」÷「89頭」=「約0.10」(百分率:約10%)
・「牡・セ」:「合計出走数に対しての割合」=「80頭」÷「89頭」=「約0.90」(百分率:約90%)
・「合計複勝数」:「合計出走数に対しての割合」=「15頭」÷「89頭」=「約0.17」(百分率:約17%)
これにより「合計出走数に対しての各割合」が分かったので、「複勝数の期待値」を計算することができます。
・「牝」:「複勝数の期待値」=「牝の割合」×「合計複勝数の割合」×「合計出走数」
=「約1.52頭」
・「牡・セ」:「複勝数の期待値」=「牡・セの割合」×「合計複勝数の割合」×「合計出走数」
=「約13.48頭」
以上より「各性別の複勝数の期待値」を計算することが出来ました。この「複勝数の期待値」を「実際の複勝数」と比較してみると、
・「牝馬」:「実際の複勝数」>「複勝数の期待値」
・「牡馬・セン馬」:「実際の複勝数」<「複勝数の期待値」
となるため、やはり「牝馬」の方が有利のように見えます。しかし、この「実際の複勝数」と「複勝数の期待値」の差が「誤差」である可能性を吟味しなければはっきりと断言できません。
そのために活用するのが「カイ二乗検定」になります。
「カイ二乗検定」による「期待値」の誤差判定
「カイ二乗検定」というのは統計検定の一種で、「カイ二乗分布」を用いて「実数値」と「理論値・期待値」の差が誤差か明確な差なのかを判定できます。「カイ二乗分布」がどういうものなのかはなかなか複雑で難しい話になってきますのでこのブログでは省かせていただきます。
気になる方は⇒https://ja.wikipedia.org/wiki/%E3%82%AB%E3%82%A4%E4%BA%8C%E4%B9%97%E5%88%86%E5%B8%83
(この他にもGoogle検索で調べれば分かりやすい解説サイトをいくつか見つけられますのでそちらをご覧ください)
判定としては「カイ二乗検定」によって計算された値が「0.05超過」である場合は「実数値」と「理論値・期待値」の差が「誤差」、「0.05以下」である場合は「明確な差」となります。
実際に上記の過去5年間の「性別」のデータの「カイ二乗検定」をExcelの関数を用いて計算すると、
・「複勝数の誤差判定」:「カイ二乗検定」=「CHISQ.TEST」=「0.20402」>「0.05」
よって、「性別」の「実際の複勝数」と「複勝数の期待値」の差は誤差の範囲であることが分かります。
ちなみに、もしもこの「性別」のデータの「カイ二乗検定」が「0.05以下」になる場合は、「牝馬の複勝数」=「4頭以上」・「牡馬・セン馬の複勝数」=「11頭以下」が条件になります。「実際の複勝数」が少し違うだけでも「誤差」ではなく「明確な差」となる場合もあるということですが、逆に言えばそれだけ大きな違いということを意味しています。
「期待値」との差が「誤差」とはどういうことか?
以上より、例題の「性別」のデータの場合は「実際の複勝数」と「複勝数の期待値」の差が「誤差」であることが分かりました。このことから、「「実際の複勝数」と「複勝数の期待値」はほぼ許容される範囲内で一致する」と言えます。
ここで考えて頂きたいこととして、「レースで複勝内に入った馬の数=複勝数」であるので「レース1つあたりの複勝数」は基本的に「3頭」です。つまり複数のレースのデータを扱っている場合、「合計複勝数」=「レース数×3頭」の比例式になるのでほぼ一定の数値になります。
よって、今回の例題の「性別」のデータの場合は「複勝数の期待値」が変動する大きな要因は「出走数」であると言えます。そして、「複勝数の期待値」≒「実際の複勝数」であることが分かっているので、「「複勝数」も「出走数」に従って変動する」ことが分かります。もし「実際の複勝数」が「出走数」ではない要因に従って変動している場合、「複勝数の期待値」と明確な差が発生するので「カイ二乗検定」の値は「0.05以下」になるはずです。よって今回の場合はほぼ断定的に「出走数」に従って変動すると言えるのです。
そのため、例題の「性別」のデータのように「牝馬の複勝率」>「牡馬・セン馬の複勝率」であったとしても、「複勝数」が「出走数」に従った量であることに変わりないため「牝馬」の方が有利である可能性が高いとは言えないのです。
実際の重賞レースのデータで「カイ二乗検定」を行うと…
ということで、以上までは例題を使った話でしたが、実際の重賞レースのデータを「カイ二乗検定」を使って判定するとどうなるのかをご紹介します。
今回はちょうど6/9に行われる「エプソムC(G3)」の過去5年間のデータを判定してました。
(「エプソムC(G3)」当日よりも前に掲載したかったのですが、間に合いませんでした…。)
データの種類は「枠番」・「年齢」・「オッズ」・「斤量馬体重比」・「馬体重」・「馬体重増減率」の6種類で、それぞれ「単勝数・連対数・複勝数」の集計と「期待値」の計算を行いExcelの関数を使って「カイ二乗検定」の数値を算出し「0.05超過」である場合は「〇」、「0.05以下」である場合は「×」としました。
枠番
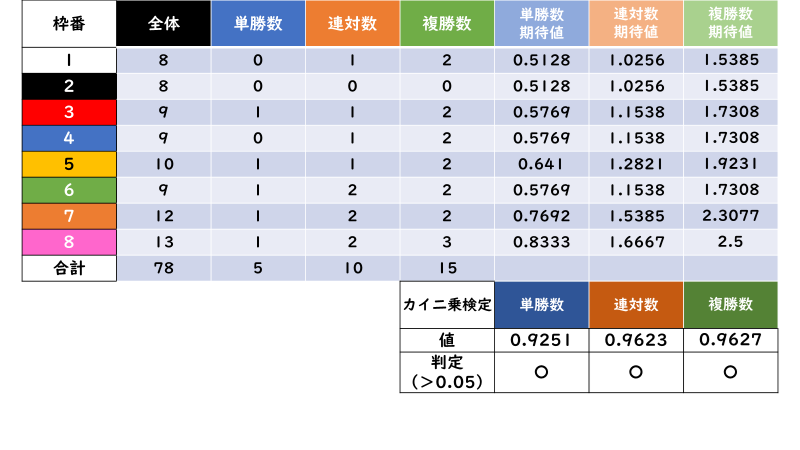
年齢
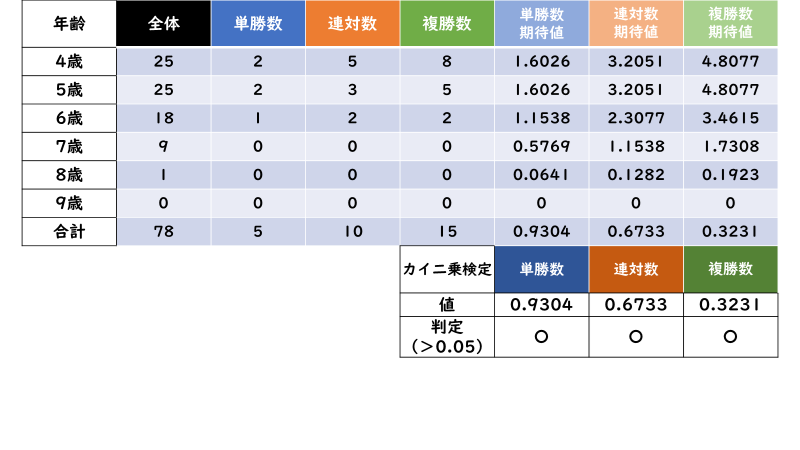
オッズ
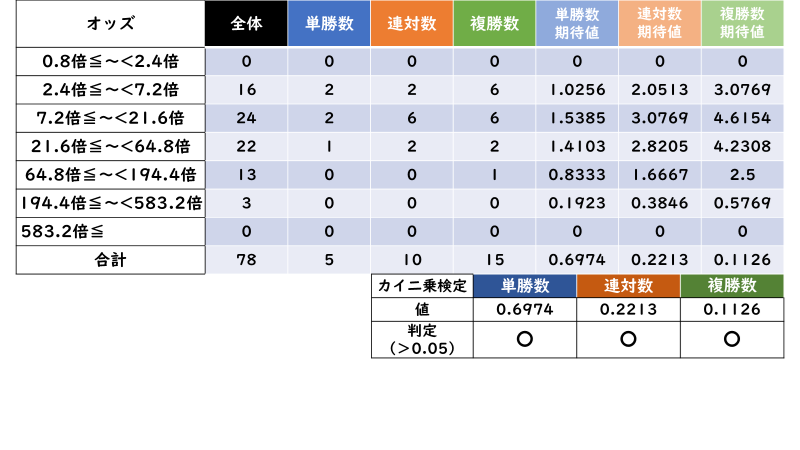
斤量馬体重比
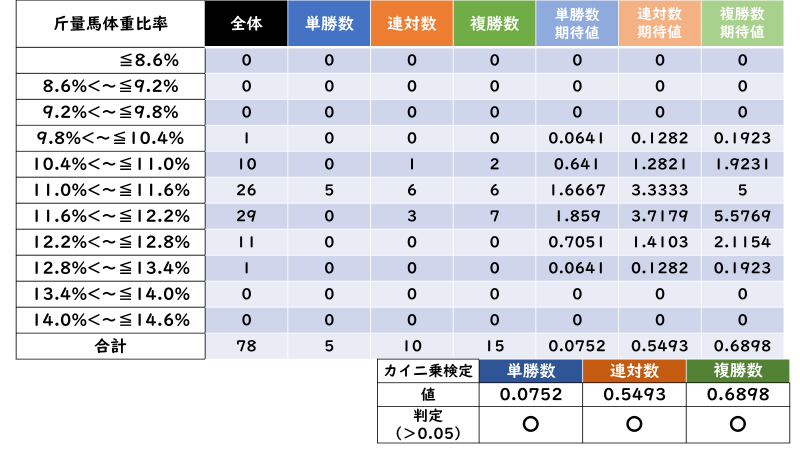
馬体重
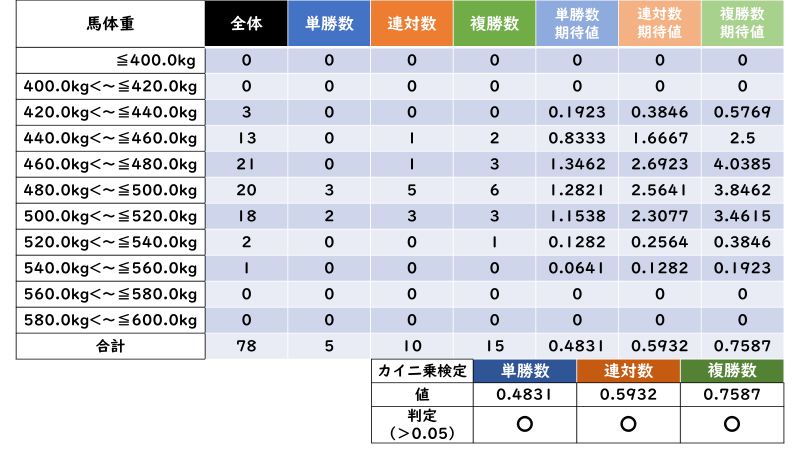
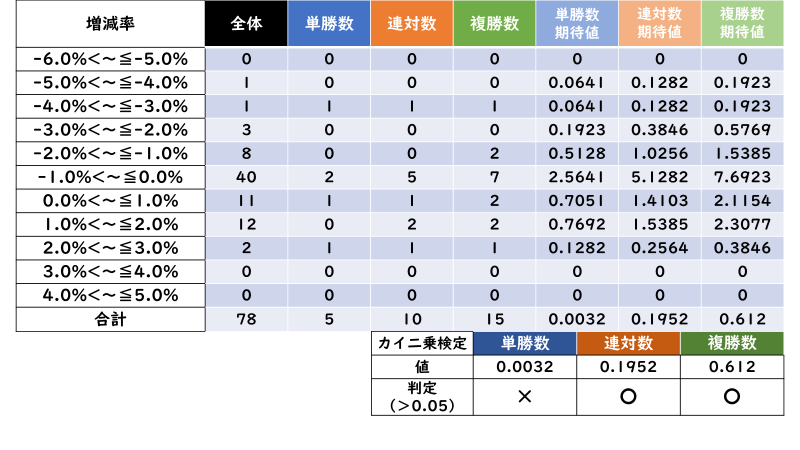
馬体重増減率
「カイ二乗検定」の結果
いかがでしょうか。「カイ二乗検定」を行った結果、ほとんどの場合で「0.05超過」であることが分かります。
つまり、大抵の場合「単勝数・連対数・複勝数の期待値」≒「実際の単勝数・連対数・複勝数」であり、「「単勝数・連対数・複勝数」は「出走数」に従って変動する」ため「「単勝率・連対率・複勝率」の比較は無意味である」と言えるのです。
Q.E.D.「複勝率」は「競馬予想おいて無意味」である
以上より、「競馬予想において単勝率・連対率・複勝率は無意味である」ということを論証できました。この結果から今後の「レース分析」の記事において「単勝率・連対率・複勝率」の傾向で解説することは控えることにします。場合によっては「カイ二乗検定」の判定が「0.05以下」になることもあるので、その場合だけは「単勝率・連対率・複勝率」を取り上げて解説する予定です。(特に「オッズ」のデータは「0.05以下」になる可能性が比較的に高いので解説で取り上げるかもしれません。)
また、「単勝数・連対数・複勝数の期待値」≒「実際の単勝数・連対数・複勝数」という関係性を証明できたことで、「過去に出走した前例があるけれども単勝・連対・複勝の経験がない属性・項目・階級」は「単勝・連対・複勝」の可能性が低い」ということでもあります。よって「0%」の場合はやはり気にした方が良いと言えそうです。
今回の記事は以上となります。ご閲覧ありがとうございました!!


